Question

The number of species n found on islands typically increases with the area of the island A. Suppose that this relationship is such that the rate of increase with island area is always proportional to the density of species (that is, number of species per unit area) with a proportionality constant k between 0 and 1. Find the function that describes the species-area relationship. (Let n(1) = n1.)

Answer 1

`n(A) = n_1A^k`

Explanation:

Taking into account that the growth rate of the number of species on the island is proportional to the density of species (number of species between area of the island), a model based on a differential equation is proposed:

`(dn)/(dA) = k(n)/(A)`

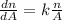
This differential equation can be solved by the method of separable variables like this:

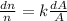`(dn)/(n) = k(dA)/(A)` with what you get:

`\int\ {(dn)/(n)}\ = k\int\ {(dA)/(A)}`

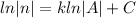`ln|n| = kln|A|+C`. Taking exponentials on both sides of the equation:

`e^(ln|n|) = e^ln`

`n(A) = e^(C)A^(k)`

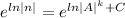
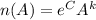
how do you have to
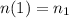`n (1) = n_1`, then

`n(A) = n_1A^k`