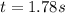Answer:
Part a)
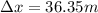
Part b)
height will be 107.2 m
Part c)
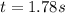
Step-by-step explanation:
Initial velocity of the ball is given as
v = 7.90 m/s
angle of projection of the ball
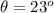
now the two components of velocity of ball is given as
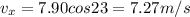
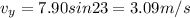
Part a)
Since ball strike the ground after t = 5 s
so the distance moved by the ball in horizontal direction is given as

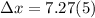
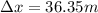
Part b)
Now in order to find the height of the ball we can find the vertical displacement of the ball
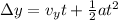
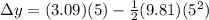

So height will be 107.2 m
Part c)
when ball reaches a point 10 m below the level of launching then the displacement of the ball is given as
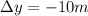
so we will have
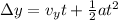
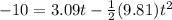
so we will have