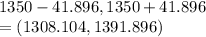Question

The number of square feet per house are normally distributed with a population standard deviation of 137 square feet and an unknown population mean. A random sample of 19 houses is taken and results in a sample mean of 1350 square feet. Find the margin of error for a 80% confidence interval for the population mean.

Answer 1

Explanation:

Given that X, the number of square feet per house is N(mean, 137)

Sample size = 19

Sample mean x bar =1350 sq ft

Since population std dev is given,

std error of sample =
`(137)/(√(19) ) \\=31.43`

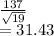
Since sample size is small, t critical value can be used

df = 18

t value for 80% two tailed = 1.333

Margin of error = ±1.333(std error) = ±
`1.333*31.43\\=41.896`

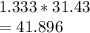
Confidence interval = sample mean ±margin of error

=
`1350-41.896,1350+41.896\\=(1308.104,1391.896)`