Question

You drop a stone into a deep well and hear it hit the bottom 6.65 s later. This is the time it takes for the stone to fall to the bottom of the well, plus the time it takes for the sound of the stone hitting the bottom to reach you. Sound travels about 343 m/s in air. How deep is the well?

Answer 1

Answer: ok, so total time is Tt = 6.65 seconds = time falling + time of sound traveling.

the time of the rock falling is given by:
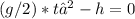`(g/2)*t₀^(2) -h = 0` (1)

where h is the heigth of the hole, and t₀ is the time it took to reach the bottom.

the time of the sound traveling is given by 343*t₁ - h = 0 (2)

so t₁ + t₀ = 6.65s = total time

then you know that t₁ = 6.65s - t₀

so now you have two variables, t₀ and h, and we want to know the value of h, so we want to write t₀ as a function of h.

in the second equation we have now: 343*(6.65 - t₀) = h

so t₀ = (-h/343 + 6.65)s

replacing this on the first equation you have:

`(g/2)*(-h/343 + 6.65)^(2) -h = 0`

now you want to take h to the right side so

w

so if we replace g by 9.8 meters over seconds square we get

h =
`\frac{-1.19 -+ \sqrt[2]{1.56} }{2*0.00041}`

where you will take the positive root

h = 61 meters