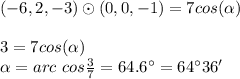Question

A million years ago, an alien species built a vertical tower on a horizontal plane. When they returned they discovered that the ground had tilted so that measurements of 3 points on the ground gave coordinates of (0,0,0),(1,3,0)(0,0,0),(1,3,0), and (0,3,2)(0,3,2). By what angle does the tower now deviate from the vertical?

Answer 1

The tower deviates
`64^\circ36'` from the vertical.

Explanation:

Having 3 point of our new plane we can construct vectors on the plane by substacting 2 of them:

`v_1=(0,3,2)-(0,0,0)\\v_2=(1,3,0)-(0,0,0)`

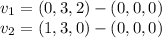
These vectors are on the plane, so a cross product between them will give us a vector perpendicular to the plane:

`(0,3,2)*(1,3,0)=\left[\begin{array}{ccc}i&j&k\\0&3&2\\1&3&0\end{array}\right] =(-6,2,-3)`

Asuming that the aliens used our conventions, the original plane was perpendicular to the z axis, so that a perpendicular vector to that plane was

(0,0,1)

We know that a dot product between 2 vectors |V.W| = |V| |W| cos(α), where α is the angle between them. If we use the vector perpendicular to this plane, and the one perpendicular to the original plane, α will represent the deviation angle of our new plane.

`\|(-6,2,-3)\|=7\\\|(0,0,1)\|=1`

`(-6,2,-3)\odot(0,0,1)= 7 cos(\alpha )\\\\ -3=7 cos(\alpha ) \\ \alpha=arc\ cos (-3)/(7) =115.37 ^\circ\\`

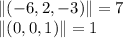
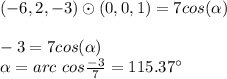
Since this angle is greater than 90 degrees it means that the vector we calculated as perpendicular to the plane points towards negative z (this can be seen by the -3 z component)

To fix this we can calculate a new perpendicular vector, or simply compare ir with the vector (0,0,-1). The latter is easier:

`(-6,2,-3)\odot(0,0,-1)= 7 cos(\alpha )\\\\ 3=7 cos(\alpha ) \\ \alpha=arc\ cos (3)/(7) =64.6^\circ =64^\circ36'`