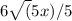Final answer:
The simplified form of the expression
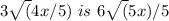 after performing the square root separately on the numerator and denominator, and then rationalizing the denominator.
after performing the square root separately on the numerator and denominator, and then rationalizing the denominator.
Step-by-step explanation:
The expression given is
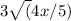 . To simplify this expression, we observe that the square root of 4 is a perfect square and equals 2. The square root of the fraction can be taken by applying the square root to the numerator and the denominator separately. Therefore, we have:
. To simplify this expression, we observe that the square root of 4 is a perfect square and equals 2. The square root of the fraction can be taken by applying the square root to the numerator and the denominator separately. Therefore, we have:
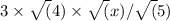
Upon simplifying, we get:
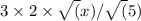
This simplifies further to:
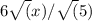
However, it's not common to leave a square root in the denominator, so we can multiply both the numerator and the denominator by sqrt(5) to rationalize the denominator.
The final simplified form is: