Question

Perform a one-proportion z-test for a population proportion. Be sure to state the hypotheses and the P-Value. State your conclusion in a sentence. In an American Animal Hospital Association survey, 37% of respondents stated that they talk to their pets on the telephone. A veterinarian found this result hard to believe, so she randomly selected 150 pet owners and discovered that 54 of them spoke to their pet on the phone. Does the veterinarian have the right to be skeptical? Perform the appropriate hypothesis test using a significance level of 5%.

Answer 1

There is not enough statistical evidence in the sample taken by the veterinarian to support his skepticism

Explanation:

To solve this problem, we run a hypothesis test about the population proportion.

Proportion in the null hypothesis
`\pi_0 = 0.37`

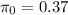
Sample size
`n = 150`

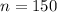
Sample proportion
`p = 54/150 = 0.36`

Significance level
`\alpha = 0.05`

`H_0: \pi_0 = 0.36\\H_a: \pi_0<0.36`

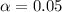
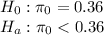
Test statistic
`= ((p - \pi_0)√(n))/(√(\pi_0(1-\pi_0)))`

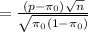
Left critical Z value (for 0.01)
`Z_(\alpha/2)= -1.64485`

Calculated statistic =
`= ((0.36 - 0.37)√(150))/(√(0.37(0.63))) = -0.254`

`p-value = 0.6003`

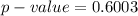
Since, test statistic is greater than critical Z, the null hypothesis cannot be rejected. There is not enough statistical evidence to state that the true proportion of pet owners who talk on the phone with their pets is less than 37%. The p - value is 0.79860.