Question

Suppose that IQ scores have a bell-shaped distribution with a mean of 97 and a standard deviation of 12. Using the empirical rule, what percentage of IQ scores are greater than 133? Please do not round your answer.

Answer 1

0.15%

Explanation:

We have been given that IQ scores have a bell-shaped distribution with a mean of 97 and a standard deviation of 12. We are asked to find the percentage of IQ scores that are greater than 133 using the empirical rule.

First of all, we will find z-score for given sample score of 133 as z-score tells us a data point is how many standard deviation away from mean.

`z=(x-\mu)/(\sigma)`, where,

`z` = Z-score,

`x` = Sample score,

`\mu` = Mean,

`\sigma` = Standard deviation.

`z=(133-97)/(12)`

`z=(36)/(12)`

`z=3`

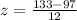
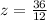
We know that according to the empirical rule 68% of data lies within one standard deviation of mean, 95% of data lies within two standard deviation of mean and 99.7% of data lies within one standard deviation of mean.

Since 133 is 3 standard deviation above mean, so 0.3% lies above and below 3 standard deviation.

Since we need IQ scores above 133, so we will divide 0.3% by 2 as:

`(0.3\%)/(2)=0.15\%`

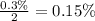
Therefore, 0.15% of IQ scores are greater than 133.