Question

Suppose you buy a new car whose advertised mileage is 20 miles per gallon​ (mpg). After driving your car for several​ months, you find that its mileage is 16.4 mpg. You telephone the manufacturer and learn that the standard deviation of gas mileages for all cars of the model you bought is 1.14 mpg. a. Find the​ z-score for the gas mileage of your​ car, assuming the advertised claim is correct. b. Does it appear that your car is getting unusually low gas​ mileage? a. zequals nothing ​(Round to two decimal places as​ needed.) b. Does it appear that your car is getting unusually low gas​ mileage? Yes No

Answer 1

a) The z-score for the mileage of the car is -3.16

b) It appears that the car is getting unusually low gas mileage.

Explanation:

The z-score formula is given by:

`Z = (X - \mu)/(\sigma)`

In which: X is the mileage per gallon we are going to find the z-score of,
`\mu` is the mean value of this mileage and
`\sigma` is the standard deviation of this value.

a. Find the​ z-score for the gas mileage of your​ car, assuming the advertised claim is correct.

The gas mileage for you car is 16.4 mpg, so
`X = 16.4`

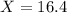
The advertised gas mileage is 20 mpg, so
`\mu = 20`

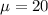
The standard deviation is 1.14 mpg, so
`\sigma = 1.14`

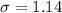
The z-score is:

`Z = (X - \mu)/(\sigma) = (16.4 - 20)/(1.14) = -3.16`

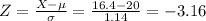
b. Does it appear that your car is getting unusually low gas​ mileage?

The general rule is that a z-score lower than -1.96 is unusually low. So yes, it appears that the car is getting unusually low gas mileage.