Question

In the following ordinary annuity, the interest is compounded with each payment, and the payment is made at the end of the compounding period. How much must you invest each month in a mutual fund yielding 11.5% compounded monthly to become a millionaire in 10 years? (Round your answer to the nearest cent.)

Answer 1

Ans. In order to become a millionaire in 10 years, you must invest in this mutual fund $4,476.21 at the end of every month, for 120 months (10 years)

Step-by-step explanation:

Hi, first, we have to transform this compound rate into an effective rate. this is as follows.

`r(EffectiveMonthly)=(r(compound monthly))/(12) =(0.115)/(12)=0.009583`

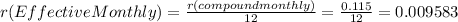
So, the effective monthly rate that we have to use is 0.9583% and the formula (Future value of an annuity) only works if the rate has the same units as the periods, therefore, we just go ahead and transform years into months. That is 10Years*12=120 months.

And now, in order to reach $1,000,000 in 10 years, we need to use the following formula.

`FutureValue=(A((1+r)^(n) -1))/(r)`

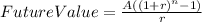
Using the data we just worked on, everything should look like this.

`1,000,000=(A((1+0.009583))^(120) -1))/(0.009583)`

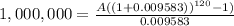
And we solve for A, as follows

`A=(1,000,000*(0.009583))/((1+0.009583)^(120)-1 ) =4,476.21`

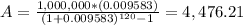
And there you go, in order to become a millionaire (reach 1,000,000) you are going to need to invest in this mutual fund $4,476.21 every month, at the end of each month, for 120 months.

Best of luck.