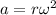Question

Use dimensional analysis to determine how the linear acceleration a in m/s2 of a particle traveling in a circle depends on some, or all, of the following properties: the radius r of the circle, the angular frequency ω in s−1 with which the particle orbits about the circle, and the mass m of the particle. There is no dimensionless constant involved in the relation.

Answer 1

I have to say, i love this kind of problems.

So, we got the linear acceleration, as we all know, linear the acceleration its, in dimensional units:

`[a]=[(distance)/(time^2)]`.

Now, we got the radius

`[r] = [distance]`

the angular frequency

`[\omega] = (1)/(s)`

and the mass

`[m]=[mass]`.

Now, the acceleration doesn't have units of mass, so it can't depend on the mass of the particle.

The distance in the acceleration has exponent 1, and so does in the radius. As the radius its the only parameter that has units of distance, this means that the radius must appear with exponent 1. Lets write

`a \propto r`.

The time in the acceleration has exponent -2 As the angular frequency its the only parameter that has units of time, this means that the angular frequency must appear, but, the angular frequency has an exponent of -1, this means it must be squared

`a \propto r \omega^2`.

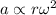We are almost there. If this were any other problem, we would write:

`a = A r \omega^2`

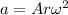
where A its an dimensionless constant. Its common for this constants to appears if we need an conversion factor. If we wanted the acceleration in cm/s^2, for example. Luckily for us, the problem states that there is no dimensionless constant involved, so:

`a = r \omega^2`