Question

Researchers measured the data speeds for a particular smartphone carrier at 50 airports. The highest speed measured was 75.6 Mbps. The complete list of 50 data speeds has a mean of x overbar equals 15.62 Mbps and a standard deviation of s equal s 20.03 Mbps.

a. What is the difference between​ carrier's highest data speed and the mean of all 50 data​ speeds?
b. How many standard deviations is that​ [the difference found in part​ (a)]?
c. Convert the​ carrier's highest data speed to a z score.
d. If we consider data speeds that convert to z scores between minus 2 and 2 to be neither significantly low nor significantly​ high, is the​ carrier's highest data speed​ significant?

Answer 1

The highest data speed recorded is 59.98 Mbps above the mean, and this difference equals approximately 2.996 standard deviations. This results in a z-score of 2.996, indicating that the carrier's highest data speed is significantly high.

Step-by-step explanation:

a. The difference between the carrier's highest data speed and the mean of all 50 data speeds is found by subtracting the mean speed from the highest speed. This is calculated as 75.6 Mbps - 15.62 Mbps = 59.98 Mbps.

b. To find out how many standard deviations this difference is, we divide the difference by the standard deviation of the data speeds: 59.98 Mbps / 20.03 Mbps = 2.996 standard deviations.

c. The z-score for the carrier's highest data speed is calculated by subtracting the mean from the data speed and then dividing by the standard deviation: (75.6 Mbps - 15.62 Mbps) / 20.03 Mbps = 2.996.

d. Since the z-score of 2.996 is greater than 2, it suggests that the carrier's highest data speed is significantly higher than what is considered neither significantly low nor high. In other words, the carrier's highest data speed is significant.

Answer 2

a) 59.98

b) 2.99

c) 2.99

d) Significantly High

Step-by-step explanation:

Part a)

Highest speed measured = x = 75.6 Mbps

Average/Mean speed =
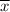`\overline{x}` = 15.62 Mbps

Standard Deviation = s = 20.03 Mbps

We need to find the difference between carrier's highest data speed and the mean of all 50 data​ speeds i.e. x -
`\overline{x}`

x -
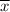
`\overline{x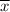}` = 75.6 - 15.62 = 59.98 Mbps

Thus, the difference between​ carrier's highest data speed and the mean of all 50 data​ speeds is 59.98 Mbps

Part b)

In order to find how many standard deviations away is the difference found in previous part, we divide the difference by the value of standard deviation i.e.

`(59.98)/(20.03)=2.99`

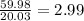
This means, the difference is 2.99 standard deviations or in other words we can say, the Carrier's highest data speed is 2.99 standard deviations above the mean data speed.

Part c)

A z score tells us that how many standard deviations away is a value from the mean. We calculated the same in the previous part. Performing the same calculation in one step:

The formula for the z score is:

`z=\frac{x-\overline{x}}{s}`

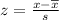
Using the given values, we get:

`z=(75.6-15.62)/(20.03)=2.99`

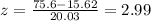
Thus, the Carriers highest data is equivalent to a z score of 2.99

Part d)

The range of z scores which are neither significantly low nor significantly​ high is -2 to + 2. The z scores outside this range will be significant.

Since, the z score for carrier's highest data speed is 2.99 which is well outside the given range, i.e. greater than 2, we can conclude that the carrier's highest data speed​ is significantly higher.