Question

There are four charges, each with a magnitude of 1.96 µC. Two are positive and two are negative. The charges are fixed to the corners of a 0.47-m square, one to a corner, in such a way that the net force on any charge is directed toward the center of the square. Find the magnitude of the net electrostatic force experienced by any charge.

Answer 1

The net electrostatic force on a charge can be found using Coulomb's law, considering the effects of both attraction and repulsion due to the charges' arrangement at the corners of a square. Calculations account for diagonal opposites and adjacent corners, taking advantage of the square's symmetry.

Step-by-step explanation:

To calculate the magnitude of the net electrostatic force on a charge in a configuration where two positive charges of 1.96 µC and two negative charges of the same magnitude are placed at the corners of a 0.47-m square, we can use Coulomb's law. Coulomb's law states that the electrostatic force (F) between two point charges is proportional to the product of the charges (q1 and q2) and inversely proportional to the square of the distance (r) between them. It is given by F = k * |q1*q2| / r², where k is Coulomb's constant (k ≈ 8.99 x 10⁹ N·m²/C²).

Since the charges are at the corners of a square, the opposing charges will attract, and like charges will repel. Each charge experiences forces due to its interaction with the other three charges. The net force on any charge is the vector sum of the forces exerted by the other three charges. This sum can be simplified as the square has symmetry so that the forces along one diagonal cancel and the forces along the sides of the square add together to pull the charge towards the center.

The diagonal distance (r) is √2 times the side of the square (a), which is r = √2 * 0.47 m. For simplicity, let's calculate the force between one charge and its diagonal opposite, and then double it for symmetry reasons (each charge has two diagonally opposite charges).

The force due to one diagonal is: F_diagonal = (k * (1.96 x 10⁻⁶)^2) / ((√2 * 0.47)²)
Now we need to calculate this force and then double it to account for both diagonals.

The final step will be to add the forces due to charges on adjacent corners, which are of the same polarity and hence exert repulsion. Their vector sum will be directed towards the square's center due to symmetry.

Answer 2

Magnitude of the resultant force (Fn₁) on q₁

Fn₁ = 0.142N (directed toward the center of the square)

Step-by-step explanation:

Theory of electrical forces

Because the particle q₁ is close to three other electrically charged particles, it will experience three electrical forces and the solution of the problem is of a vector nature.

Graphic attached

The directions of the individual forces exerted by q₂, q₃ and q₄ on q₁ are shown in the attached figure.

The force (F₁₄) of q₄ on q₁ is repulsive because the charges have equal signs and the forces (F₁₂) and (F₁₃) of q₂ and q₃ on q₁ are attractive because the charges have opposite signs.

Calculation of the forces exerted on the charge q₁

To calculate the magnitudes of the forces exerted by the charges q₂, q₃, and q₄ on the charge q₁ we apply Coulomb's law:

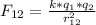`F_(12) = (k*q_1*q_2)/(r_(12)^2)`: Magnitude of the electrical force of q₂ over q₁. Equation((1)

`F_(13) = (k*q_1*q_3)/(r_(13)^2)`: Magnitude of the electrical force of q₃ over q₁. Equation (2)

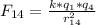`F_(14) = (k*q_1*q_4)/(r_(14)^2)`: Magnitude of the electrical force of q₄ over q₁. Equation (3)

Equivalences

1µC= 10⁻⁶ C

Known data

q₁=q₄= 1.96 µC = 1.96*10⁻⁶C

q₂=q₃= -1.96 µC = -1.96*10⁻⁶C

r₁₂= r₁₃ = 0.47m: distance between q₁ and q₂ and q₁ and q₄

`r_(14) = √(0.47^2+ 0.47^2)=0.664m`

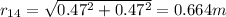
k=8.99x10⁹N*m²/C² : Coulomb constant

F₁₂ calculation

We replace data in the equation (1):

`F_(12) = (8.99*10^9*(1.96*10^(-6))^2)/(0.47^2)`

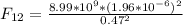
F₁₂ = 0.156 N Direction of the positive x axis (+x)

F₁₃ calculation

We replace data in the equation (2):

`F_(13) = (8.99*10^9*(1.96*10^(-6))^2)/(0.47^2)`

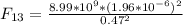
F₁₃ = 0.156 N Direction of the negative y axis (-y)

Magnitude of the net electrostatic force between F₁₃ and F₁₂

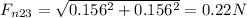`F_(n23)= √(0.156^2+0.156^2) = 0.22N` (directed toward the center of the square)

F₁₄ calculation

We replace F₁₄ data in the equation (3):

`F_(14) = (8.99*10^9*(1.96*10^(-6))^2)/(0.664^2)`

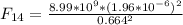
F₁₄ = 0.078 N (In the opposite direction to Fn₂₃)

Calculation of the resulting force on q₁: Fn₁

Fn₁ = Fn₂₃ - F₁₄ = 0.22 - 0.078 = 0.142 N