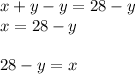Question

Sophie is buying fabric to make items for a craft fair. The table shows some combinations of how much of each color fabric she might buy. Which equations model the total yards of fabric Sophie will buy? Check all that apply.

A. X+Y=28
B. 28+X=Y
C. X-Y=28
D. 28-X=Y
E. 28-Y=X

Answer 1

A,D, and E

Explanation:

Answer 2

OPTION A.

OPTION D.

OPTION E.

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

The Standard form of the equation of the line is:

`Ax + By = C`

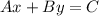
Where "A" is a positive integer, and "B" and "C" are integers.

Choose two points from the table and find the slope with this formula:

`m=(y_2-y_1)/(x_2-x_1)`.

Points:

`(1,27)\\\\(4,24)`

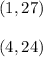
So we get that the slope is:

`m=(24-27)/(4-1)=-1`

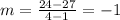
Let's substitute the slope and the coordinates of the point (1,27) into
`y=mx+b` and then solve for "b":

`27=(-1)(1)+b\\\\27+1=b\\\\b=28`

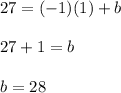
Then, we get that the equation of the line in Slope-Intercept form is:

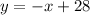`y=-x+28` or
`28-x=y`

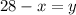
In order to write it in Standard form, we can add "x" to both sides of the equation:

`y+x=-x+28+x\\\\x+y=28`

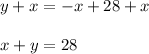
We can solve for "x" by subtracting "y" from both sides of the equation:

`x+y-y=28-y\\x=28-y\\\\28-y=x`