Question

The probability that a customer's order is not shipped on time is 0.06. A particular customer places three orders, and the orders are placed far enough apart in time that they can be considered to be independent events. Round your answers to four decimal places.

(a) What is the probability that all are shipped on time?
(b) What is the probability that exactly one is not shipped ontime?
(c) What is the probability that two or more orders are not shipped on time?

Answer 1

a) There is a 83.06% probability that all orders are shipped on time.

b) There is a 15.90% probability that exactly one order is not shipped ontime.

c) The probability of at least two orders being late is 1.02% + 0.02% = 1.04%.

Explanation:

Probability:

What you want to happen is the desired outcome.

Everything that can happen iis the total outcomes.

The probability is the division of the number of possible outcomes by the number of total outcomes.

In our problem, there is:

-A 6% probability that a customer's order is not shipped on time.

-A 94% probability that a customer's order is shipped on time.

We have these following orders:

O1 - O2 - O3.

(a) What is the probability that all are shipped on time?

The probabilities that each order is shipped on time are O1 = 0.94, O2 = 0.94 and O3 = 0.94. So:

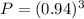`P = (0.94)^(3)` = 0.8306

There is a 83.06% probability that all orders are shipped on time.

(b) What is the probability that exactly one is not shipped ontime?

The order's can be permutated. What this means? It means that we can have O1 late and O2,03 on time, O2 late and O1,O3 on time and O3 late and O1, O2 on time. We have a permutation of 3 elements(the orders) with 2 and 1 repetitions(2 on time and one late).

The probability that an order is late is:

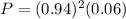`P = (0.94)^(2)(0.06)` = 0.053 for each permutation

Considering the permutations:

`P = 0.053*p^(3)_(2,1) = 0.053(3!)/(2!*1!) = 0.053*3 = 0.1590`

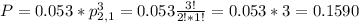
There is a 15.90% probability that exactly one order is not shipped ontime.

(c) What is the probability that two or more orders are not shipped on time?

P = P1 + P2, where P1 is the probability that two orders are late and P3 is the probability that all three orders are late.

P1

Considering the permutations, the probability that two orders are late is:

`P_(1) = p^(3)_(2,1)*(0.94)*(0.06)^(2) = 3*(0.94)*(0.06)^(2) = 0.0102`

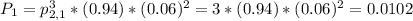
There is a 1.02% probability that two orders are late

P2

`P_(2) = (0.06)^3 = 0.0002`

There is a 0.02% probability that all three orders are late.

The probability of at least two orders being late is 1.02% + 0.02% = 1.04%.