Question

Suppose you are in a game show and there are 10 doors in front of you. You know that there is a prize behind one of them, and nothing behind the other 9. You have to choose a door containing the prize in order to win the prize. However, before you choose, the game show host promises that rather than immediately opening the door of your choice to reveal its contents, he will open one of the other 9 doors to reveal that it is an empty door. He will then give you the option to change your choice. You may assume that the host is completely impartial – not malicious in any way. For instance, if you choose door 3, he will open one door, say door 5, to reveal that it is empty. Should you continue with door 3 or choose another door? Please compute the probability of finding the prize behind your chosen door before the game show host reveals that one door is empty, and the probability of you finding the prize by changing to a different door after seeing the revealed empty door.

Answer 1

The probabilities are
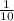`(1)/(10)` and
`(9)/(80)`

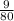
Explanation:

There are 10 doors. 9 of wich have no prizes and 1 with the prize. So the probability to choose the winner one is 1 out of 10. So:

The probability of finding the prize behind your chosen door before the game show host reveals that one door is empty is
`(1)/(10)`.

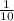Now. If the game show host opens one of the other 9 doors to reveal that it is an empty door, there are 2 posibilities:

1) Do not change your chosen door: In this case the probability reamins the same,
`(1)/(10)`.

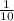2) Change your chosen door. Lets compute the probability to loose: There are two posibilities.

2a) If your initial door is the one with the prize. In this case you are going to loose (because you will change your door). The probability for this to happen is
`(1)/(10)`.

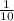2b) If your initial door is not the one with the prize (the probability of this is
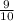`(9)/(10)`). In this case we will loose if, after the game show host opens an empty door, we choose an empty door. The probability of choosing an empty door in this case is
`(7)/(8)`.

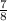So the probability to loose is:

`(1)/(10)+(7)/(8)(9)/(10)=(1)/(10)+(63)/(80)=(71)/(80)`

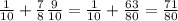
Then, the probability to win is
`1-(71)/(80)=(9)/(80)>(1)/(10)`

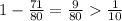
In conclusion: Changing the door improves the probability to win.