Question

Find each of the following functions. f(x) = 5 − x , g(x) = x2 − 9 (a) f + g State the domain of the function. (Enter your answer using interval notation.) (b) f − g State the domain of the function. (Enter your answer using interval notation.) (c) fg Incorrect: Your answer is incorrect. State the domain of the function. (Enter your answer using interval notation.) (d) f/g State the domain of the function. (Enter your answer using interval notation.)

Answer 1

The sum, difference, product, and quotient of two functions f(x) = 5 - x and g(x) = x^2 - 9 can be found by adding, subtracting, multiplying, and dividing their corresponding terms. The domain of each resulting function can be determined by considering the domain of the original functions and any restrictions imposed by the operations involved.

Step-by-step explanation:

(a) f + g

To find the sum of two functions, we simply add the corresponding terms. So, f + g = (5 - x) + (x^2 - 9).

Simplifying, we get f + g = x^2 - x - 4.

The domain of the function f + g is the intersection of the domains of f and g. Since both f and g are defined for all real numbers, the domain of f + g is also all real numbers, which can be represented as (-∞, ∞) in interval notation.

(b) f - g

To find the difference of two functions, we subtract the corresponding terms. So, f - g = (5 - x) - (x^2 - 9).

Simplifying, we get f - g = -x^2 + x + 14.

Similar to part (a), the domain of the function f - g is all real numbers, which can be represented as (-∞, ∞) in interval notation.

(c) fg

To find the product of two functions, we multiply the corresponding terms. So, fg = (5 - x)(x^2 - 9).

Simplifying, we get fg = -x^3 + 9x - 5x^2 + 45.

Similar to parts (a) and (b), the domain of the function fg is all real numbers, which can be represented as (-∞, ∞) in interval notation.

(d) f/g

To find the quotient of two functions, we divide the corresponding terms. So, f/g = (5 - x)/(x^2 - 9).

However, we need to consider the values of x that make the denominator zero, since division by zero is undefined. In this case, the denominator x^2 - 9 is equal to zero when x = ±3.

Therefore, the domain of the function f/g is all real numbers except x = ±3. In interval notation, this can be represented as (-∞, -3) ∪ (-3, 3) ∪ (3, ∞).

Answer 2

a, b and c= (-∞,∞) d = (-∞,3) U (-3,3) U (3,∞)

Step-by-step explanation:

Hi there!

1) Firstly, let's recap the sum of functions rule:

f(x) + g(x) = (f+g)(x)

Applying it to those functions, we have:

f(x)=5-x +g(x)=
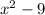`x^(2) -9` = [(5-x) +(
`x^(2)`-9)](x)

(f+g)(x)=
`5-x+x^(2) -9`

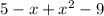
2) To State the Domain is to state the set which is valid the quantities of x, of a function. In this case,

a) (f+g)(x)= 5-x+
`x^(2)`+9

Simplifiying

(f+g)(x) =
`x^(2) -x+4=0`

Since there are no restrictions neihter discontinuities, this function has a Domain which can expressed this way:

X may assume infinite quantities, negatives or positives one in the Real set.

(-∞< x <∞+) or simply (-∞,∞)

Or simply put, x ∈ R. Remember, ∞ is not a number, it's a notation meaning infinite values. That's why it's not a closed interval.

Check the graph below.

b) (f-g)(x) =(5-x) -(x²-9)

(f-g)(x)= 5-x-x²+9

Domain of (f-g)(x) =x²-x+14

Similarly to a) this function (f-g)(x) has not discontinuity, nor restrictions on its Domains.

Since there are no restrictions either discontinuities, this function has a Domain which can be expressed this way:

X may assume infinite quantities, negatives or positives one in the Real set.

(-∞< x <∞ +) then finally, the answer: (-∞,∞)

c) (f*g)(x)=(5-x)(x²-9)

(f*g)(x)=5x²-45-x³+9x

Again, this function has no discontinuities, nor restrictions in its Domain as you can check it on its graph.

Then, the Domain of (f*g)(x)=(5-x)(x²-9) is also (-∞,∞)

d) (f/g)(x) =(5-x)/(x²-9)

Highlighting the denominator, we can calculate the Domain.

We can see a restriction here. There is no denominator zero, defined for the Set of R.

Then, let's calculate

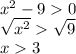`x^(2) -9>0\\ √(x^2) >√(9)\\x>3` and x < -3

In the Numerator, no restrictions.

So the Domain will be the union between the Numerator's Domain and the Denominator's Domain with Restrictions.

Check the graph below.

Finally

D = (-∞,3) U (-3,3) U (3,∞)