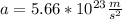Question

Suppose a single electron orbits about a nucleus containing two protons (+2e), as would be the case for a helium atom from which one of the naturally occurring electrons is removed. The radius of the orbit is 2.99 × 10-11 m. Determine the magnitude of the electron's centripetal acceleration.

Answer 1

`a=5.66*10^(23) (m)/(s^2)`

Step-by-step explanation:

In this case we will use the Bohr Atomic model.

We have that:
`F=m*a`

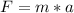
We can calculate the centripetal force using the coulomb formula that states:

`F=k*(q*q')/(r^2)`

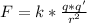
Where K=
`9*10^9 (Nm^2)/(C)`

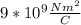
and r is the distance.

Now we can say:

`m*a=k*(q*q')/(r^2)`

The mass of the electron is =
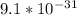`9.1*10^(-31)` Kg

The charge magnitud of an electron and proton are=
`1.6*10^(-19)C`

Substituting what we have:

`[tex]a=(9*10^(9)*(1.6*10^(-19) )*(2(1.6*10^(-19) )))/(9.1*10^(-31)*(2.99*10^(-11))^2 )`[/tex]

so:

`a=5.66*10^(23) (m)/(s^2)`