Question

Suppose A, B, and C are mutually independent events with probabilities P(A) = 0.5, P(B) = 0.8, and P(C) = 0.3. Find the probability that exactly two of the events A, B, C occur.

Answer 1

By the law of total probability,

`P(A\cap B)=P[(A\cap B)\cap C]+P[(A\cap B)\cap C']`

but the events A, B, and C are mutually independent, so

`P(A\cap B)=P(A)P(B)`

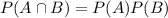
and the above reduces to

`P(A)P(B)=P(A)P(B)P(C)+P(A\cap B\cap C')\implies P(A\cap B\cap C')=P(A)P(B)(1-P(C))=P(A)P(B)P(C')`

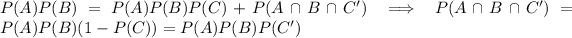
which is to say A, B, and C's complement are also mutually independent, and so

`P(A\cap B\cap C')=0.5\cdot0.8\cdot(1-0.3)=0.12`

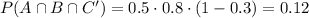
By a similar analysis,

`P(A\cap B'\cap C)=P(A)P(B')P(C)=0.03`

`P(A'\cap B\cap C)=P(A')P(B)P(C)=0.12`

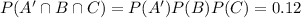
These events are mutually exclusive (i.e. if A and B occur and C does not, then there is no over lap with the event of A and C, but not B, occurring), so we add the probabilities together to get 0.27.