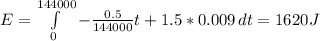Question

The manufacturer of a 1.5 V D flashlight battery says that the battery will deliver 9 mA for 40 continuous hours. During that time, the voltage will drop from 1.5 V to 1.0 V. Assume the drop in voltage is linear with time. (2 points) How many seconds is 40 hrs? (5 points) Plot the battery voltage as a function of time. Each axis needs a label (what is being plotted), scale (the values along the axis), and units. (7 points) Plot the battery power as a function of time. Write an equation for the power from 0 hours to 40 hours. (6 points) Remember that power is the derivative of energy with respect to time so energy is the integral of power over a given time period. There are two ways to find the energy. One is to calculate the area under the power curve from 0 hours to 40 hours. The second is to perform the integration of the power function from 0 to 40 hours. Find how much energy does the battery delivers in this 40 hour interval using both methods. The numerical answer is 1620 J. You must show the correct method to get credit.

Answer 1

a) 144.000 s

b) and c)Battery voltage and power plots in attached image.

`V=-(0.5)/(144000) t + 1.5 V[tex]</strong></p><p>    <strong>[tex]P(t)=-(31.25X10^(-9)) t+0.0135` where D:{0<t<40} h

d) 1620 J

Explanation:

a) The first answer is a rule of three

`s=(3600s * 40h)/(1h) = 144000s`

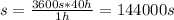
b) Using the line equation with initial point (0 seconds, 1.5 V)

`m=(1-1.5)/(144000-0) = (-0.5)/(144000)`

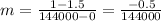
where m is the slope.

`V-V_(1)=m(x-x_(1))`

where V is voltage in V, and t is time in seconds

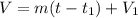`V=m(t-t_(1)) + V_(1)` and using P and m.

d) Having a count that.

`E = \int\limits^(144000)_(0) {P(t)} \, dt  = \int\limits^(144000)_(0) {v(t)*i(t)} \, dt`

`E = \int\limits^(144000)_(0) {-(0.5)/(144000) t + 1.5*0.009} \, dt = 1620 J`