Question

An object moving due to gravity can be described by the motion equation y=y0+v0t−12gt2, where t is time, y is the height at that time, y0 is the initial height (at t=0), v0 is the initial velocity, and g=9.8m/s2 (the acceleration due to gravity). If you stand at the edge of a cliff that is 75 m high and throw a rock directly up into the air with a velocity of 20 m/s, at what time will the rock hit the ground? (Note: The Quadratic Formula will give two answers, but only one of them is reasonable.)

Answer 1

`t=6.4534 s`

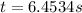
Step-by-step explanation:

This is an exercise where you need to use the concepts of free fall objects

Our knowable variables are initial high, initial velocity and the acceleration due to gravity:

`y_(0)=75m`

`v_(oy) =20m/s`

`g=9.8 m/s^(2)`

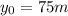
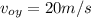
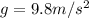
At the end of the motion, the rock hits the ground making the final high y=0m

`y=y_(o)+v_(oy)*t-(1)/(2)gt^(2)`

If we evaluate the equation:

`0=75m+(20m/s)t-(1)/(2)(9.8m/s^(2))t^(2)`

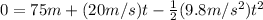
This is a classic form of Quadratic Formula, we can solve it using:

`t=\frac{-b ± \sqrt{b^(2)-4ac } }{2a}`

`a=-4.9\\b=20\\c=75`

`t=\frac{-(20) + \sqrt{(20)^(2)-4(-4.9)(75) } }{2(-4.9)}=-2.37s`

`t=\frac{-(20) - \sqrt{(20)^(2)-4(-4.9)(75) } }{2(-4.9)}=6.4534s`

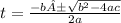
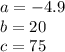
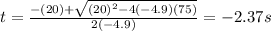
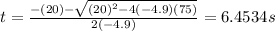
Since the time can not be negative, the reasonable answer is

`t=6.4534s`