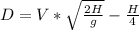Question

A package is dropped from an airplane flying horizontally with constant speed V in the positive xdirection. The package is released at time t = 0 from a height H above the origin. In addition to the vertical component of acceleration due to gravity, a strong wind blowing from the right gives the package a horizontal component of acceleration of magnitude ¼g to the left. Derive an expression for the horizontal distance D from the origin where the package hits the ground.

Answer 1

`D=V*\sqrt{(2H)/(g) } -(H)/(4)`

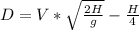
Step-by-step explanation:

From the vertical movement, we know that initial speed is 0, and initial height is H, so:

`Y_(f)=Y_(o)-g*(t^(2))/(2)`

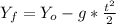
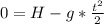`0=H-g*(t^(2))/(2)` solving for t:

`t=\sqrt{(2H)/(g) }`

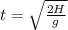
Now, from the horizontal movement, we know that initial speed is V and the acceleration is -g/4:

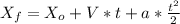`X_(f)=X_(o)+V*t+a*(t^(2))/(2)` Replacing values:

`D=V*\sqrt{(2H)/(g) }-(g)/(4)*(1)/(2) *(\sqrt{(2H)/(g) })^(2)`

Simplifying:

`D=V*\sqrt{(2H)/(g) } -(H)/(4)`