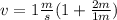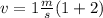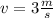Question

A student is walking with a constant speed of ????????1meters per second along High Street and sees a puddle ????????1 meters ahead of her. A bus driver is driving parallel to the student along High Street as well. At the moment the bus is ????????2meters behind the student, the bus driver decides he wants to splash he student with water by driving over the puddle as the student walks past. Determine the expression for the speed that the bus must have in terms of the given variables such that the bus and the student reach the puddle at the same time to splash the student.

Answer 1

• The expression is

`v= v_(student) ( 1 + (d_(bus \ to \ the \ student))/(d_(student \ to \ puddle)) )`

• The speed must be 3 m/s

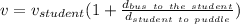
Step-by-step explanation:

We know that speed is:

`v= (distance)/(time)`.

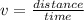So, to find the speed for the bus, we need to know:

• a. How far the bus is from the puddle.

• b. In how much time will the student reach the puddle.

Lets call
`v_(student)` the speed of the student, and
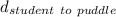`d_(student \ to \ puddle)` the distance from the student to the puddle.

We can obtain the time taking

`v_(student)= \frac {d_student \ to \ puddle}{t}`

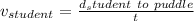
as t must be the time that the student will take to reach the puddle:

`t= \frac {d_(student \ to \ puddle)}{v_(student)}`

The bus is at a distance
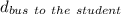`d_(bus \ to \ the \ student)` behind the student, so, the total distance that the bus must travel to the puddle is:

`d_(bus \ to \ the \ puddle) = d_(bus \ to \ the \ student) + d_(student \ to \ puddle)`

Taking all this togethes, the formula must be:

`v= (d_(bus \ to \ the \ puddle))/(t)`.

`v= \frac{d_(bus \ to \ the \ student) + d_(student \ to \ puddle)}{\frac {d_(student \ to \ puddle)}{v_(student)}}`.

`v= v_(student) (d_(bus \ to \ the \ student) + d_(student \ to \ puddle))/(d_(student \ to \ puddle))`.

`v= v_(student) ((d_(bus \ to \ the \ student))/(d_(student \ to \ puddle)) + (d_(student \ to \ puddle))/(d_(student \ to \ puddle)) )`.

`v= v_(student) ( 1 + (d_(bus \ to \ the \ student))/(d_(student \ to \ puddle)) )`.

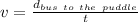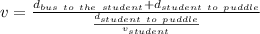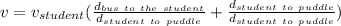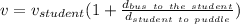And this is the formula we are looking for.

Taking the values from the problem, we find

`v= 1 (m)/(s) ( 1 + (2 m)/(1 m))`

`v= 1 (m)/(s) ( 1 + 2)`

`v= 3 (m)/(s)`