Answer:
Step-by-step explanation:
For elestic collision
v₁ =
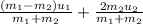
u_2)/(m_1+m_2) +(2m_1u_1)/(m_1+m_2)](https://img.qammunity.org/2020/formulas/physics/college/iojv2btxpg6dcgyh3is3cxfkhqn2tv0pg7.png) [/tex]
[/tex]
Here u₁ = 0 , u₂ = 22 m/s , m₁ = 77 kg , m₂ = .15 kg , v₁ and v₂ are velocity of goalie and puck after the collision.
v₁ = 0 + ( 2 x .15 x22 )/ 77.15
= .085 m / s
Velocity of goalie will be .085 m/s in the direction of original velocity of ball before collision.
v₂ = (.15 - 77)x 22 / 77.15 +0
= - 21.91 m /s
=Velocity of puck will be - 21.91 m /s in the direction opposite to original velocity of ball before collision.