Question

The Riverwalk in San Antonio, Texas has several arched pedestrian bridges that cross the San Antonio River. These arches are the arcs of circles. The distance across the river at this bridge is 150 feet, and the height in the center of the arch, above the water is 30 feet. Determine the radius of the circle. Note that the diameter of the circle is not 150 feet.

Answer 1

Answer: radius = 108.75 feet

Hi!

In the drawing you can see the arch that goes from point A to B. The right line from A to B is the length L = 150 feet, across the river. The height is h = 30 feet.

There is a right triangle with hypotenuse R, and the legs are (R-h), and L/2. The Pythagorean theorem says that:

`R^2 = (R-h)^2 + ((L)/(2)) ^2 = R^2 -2hR + h^2 + ((L)/(2)) ^2\\`

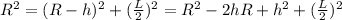
Then:

`0 = -2hR + h^2 +((L)/(2)) ^2\\R = (h^2 +((L)/(2)) ^2)(1)/(2h)`

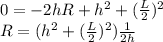
Plugging the values of L and h, you get R = 108.75 feet