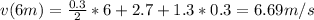Question

The acceleration of a particle which is moving along a straight line is given by a = –kv0.5, where a is in meters per second squared, k is a constant, and v is the velocity in meters per second. Determine the velocity as a function of both time t and position s. Evaluate your expressions for t = 2.7 sec and at s = 6 m, if k = 0.3 m0.5 sec–1.5 and the initial conditions at time t = 0 are s0 = 2.6 m and v0 = 2.7 m/sec.

Answer 1

`v(t)=2.7*e^(0.5kt)\\\\ v(s)=(k)/(2)*s+2.7-1.3k\\\\`

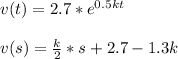
For t=2.7s and k=0.3 m/s:

`v(2.7s)=1.80m/s`

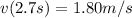
For s=6m and k=0.3 m/s:

`v(6m)=6.69m/s\\\\`

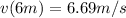
Step-by-step explanation:

Definition of acceleration:

`a=(dv)/(dt) =0.5kv`

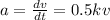
we integrate in order to find v(t):

`(dv)/(v) =-0.5kdt`

`\int\limits^v_0 { (dv)/(v)} \, =-0.5k\int\limits^t_0 {dt} \,`

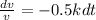
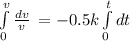
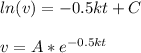`ln(v)=-0.5kt+C\\\\ v=A*e^(-0.5kt)` A=constant

Definition of velocity:

`v=(ds)/(dt) =A*e^(-0.5kt)`

We integrate:

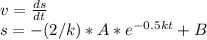`v=(ds)/(dt) \\s=- (2/k)*A*e^(-0.5kt)+B` B=constant

But:

`v=A*e^(-0.5kt)`⇒
`s= -(2/k)*v+B`

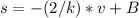
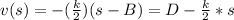`v(s)=-((k)/(2) )(s-B)=D-(k)/(2)*s` D=other constant

Initial conditions:t = 0 are s0 = 2.6 m and v0 = 2.7 m/sec:

`v(t)=A*e^(-0.5kt)\\ 2.7=Ae^(-0.5k*0)\\ 2.7=A\\`

`v(s)=D-(k)/(2)*s\\2.7=D-(k)/(2)*2.6\\D=2.7+1.3k`

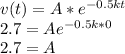
So:

`v(t)=2.7*e^(-0.5kt)\\\\ v(s)=(k)/(2)*s+2.7+1.3k\\\\`

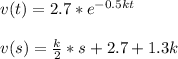
For t=2.7s and k=0.3 m/s:

`v(2.7s)=2.7*e^(-0.5*0.3*2.7)=1.80m/s`

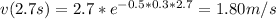
For s=6m and k=0.3 m/s:

`v(6m)=(0.3)/(2)*6+2.7+1.3*0.3=6.69m/s\\\\`