Question

A company issues $25300000, 7.8%, 20-year bonds to yield 8.0% on January 1, Year 17. Interest is paid on June 30 and December 31. The proceeds from the bonds are $24799240. Using effective-interest amortization, what will the carrying value of the bonds be on the December 31, Year 17 balance sheet?

Answer 1

Ans. The carrying value of this bond on Dec. 31/17 is $25,185,800.90

Step-by-step explanation:

Hi, the carrying value of this debt depends on the unpaid coupons and its principal, and since 2 semi-annual coupons were already paid, we have to bring to present value (to Dec /17) the remaining coupons and the principal to be paid. The formula is as follows.

`Carrying Value=(Coupon((1+r)^(n-1)-1) )/(r(1+r)^(n-1) ) +(FaceValue+Coupon)/((1+r)^(n) )`

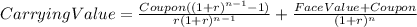
Where:

`Coupon=25,300,000*(0.078)/(2) =986,700`

`Yield(semi-annual)=(1+0.08)^{(1)/(2) } -1=0.03923`

`n=20years*2-2(paid coupons)=38`

`Carrying Value=(986,700((1+0.03923)^(37)-1) )/(0.03923(1+0.03923)^(37) ) +(25,300,000+986700)/((1+0.03923)^(38) )`

`Carrying Value=25,185,800.90`

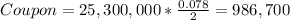
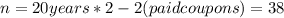
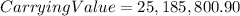
Best of luck.