Question

QUESTION 6

a) A particle moves along a horizontal line according to the equation:
x = 2t2 + 3t -5,
where x is the displacement in m) at time t (in seconds).
Find the velocity and acceleration at an instant when time is 5 seconds.
(6 marks)
b) If distance S travelled by an object in time t is given by:
S = e3t
(i) Calculate displacement at t = 0 seconds.
[2 marks]
(ii) Prove that the acceleration is nine times distance.
(6 marks]
c) Find the area enclosed by the curve y = sin 2x, the x-axis and the ordinates
x = 0 and x = T.
[6 marks​

Answer 1

(a) The instant velocity and acceleration at a specific time
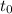`t_0` are given by evaluating the first and second derivatives at
`t=t_0`

So, we have

`\begin{cases}x(t)=2t^2+3t-5\\x'(t)=4t+3\\x''(t)=4\end{cases}`

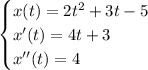
Which implies

`\begin{cases}x'(5)=23\\x''(5)=4\end{cases}`

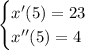
So, when time is 5 seconds, the object has a velocity of 23 m/s and an acceleration of 4 m/s^2 (which is indeed constant along all motion).

(b) The equation for the displacement is already given:
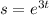`s=e^(3t)`. So, we simply have to evaluate this function at t=0 to get

`s(0)=e^(3\cdot 0)=e^0=1`

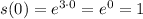
So, the displacement at t=0 is 1 unit along the positive side of the line.

As for the acceleration, applying the derivation formula

`(d)/(dx) e^(f(x)) = e^(f(x))\cdot f'(x)`

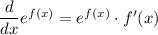
we have

`s'(t) = 3e^(3t),\quad s''(t) = 3\cdot 3e^(3t)=9e^(3t)`

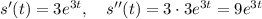
So, we have

`s(t) = e^(3t),\quad s''(t) =9e^(3t)`

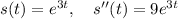
and thus the acceleration is nine times the distance.

(c)

We have to evaluate the integral

`\displaystyle \int_0^T \sin(2x)`

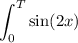
The antiderivative of sin(2x) is -1/2cos(2x), becase we have

`(d)/(dx) -(1)/(2)\cos(2x) = (1)/(2)2\sin(2x)=\sin(2x)`

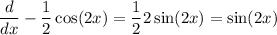
So, we have

`\displaystyle \int_0^T \sin(2x) = \left[-(1)/(2)\cos(2x)\right]_0^T = -(1)/(2)\cos(2T)+(1)/(2)\cos(0)=(1-\cos(2T))/(2)`