Question

Classify each of the power functions based on their end behavior (increasing or decreasing) as x = ∞


`f(x) = - 2 {x}^(2)`

`g(x) = (x + 2 {)}^(3)`

`h(x) = - 1 +x(1)/(2)`

`j(x) = (1)/(2) ( - {x})^(5)`
​

Answer 1

Answer: right side behavior:

f(x) is Decreasing

g(x) is Increasing

h(x) is Increasing

j(x) is Decreasing

Explanation:

The rules for end behavior are based on 2 criteria: Sign of leading coefficient and Degree of polynomial

Sign of leading coefficient (term with greatest exponent):

• If sign is positive, then right side is increasing
• If sign is negative, then right side is decreasing

Degree of polynomial (greatest exponent of polynomial:

• If even, then end behavior is the same from the left and right
• If odd, then end behavior is opposite from the left and right

f(x) = -2x²

• Sign is negative so right side is decreasing
• Degree is even so left side is the same as the right side (decreasing)

as x → +∞, f(x) → +∞ Decreasing

as x → -∞, f(x) → -∞ Decreasing

g(x) = (x + 2)³

• Sign is positive so right side is increasing
• Degree is odd so left side is opposite of the right side (decreasing)

as x → +∞, f(x) → +∞ Increasing

as x → -∞, f(x) → -∞ Decreasing

`h(x)=-1+x^{(1)/(2)}\implies h(x)=x^{(1)/(2)}-1`

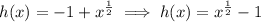
• Sign is positive so right side is increasing
• Degree is an even fraction so left side is opposite of the right side as it approaches the y-intercept (-1)

as x → +∞, f(x) → +∞ Increasing

as x → -∞, f(x) → -1 Decreasing to -1

`j(x)=(1)/(2)(-x)^5\implies j(x)=(1)/(2)(-1)^5(x)^5\implies j(x)=-(1)/(2)x^5`

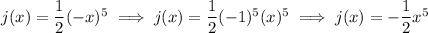
• Sign is negative so right side is decreasing
• Degree is odd so left side is opposite of the right side (increasing)

as x → +∞, f(x) → +∞ Decreasing

as x → -∞, f(x) → -∞ Increasing