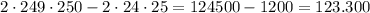Question

Find the sum of all three digits multiples of 4.
Class 10 CBSE Arthmetic progressions.

Answer 1

First 3 digit multiple = 100

Last 3 digit multiple = 996

AP: 100, 104, 108...996

an = 996

a + (n-1)d = 996

100 + (n-1)4 = 996

(n-1)4 = 896

(n-1) = 224

Therefore n = 225

Sn = n(a+l)/2

= 225(100+996)/2

= 225 x 548

= 123300

Hope this helps!

Answer 2

Multiples of 4 can be written as 4k, for some integer k.

The first three digits multiple of 4 is 4*25=100, and the last is 4*249=996.

So, the sum of all the three digits multiples of 4 is

`\displaystyle \sum_(k=25)^(249)4k = 4\sum_(k=25)^(249)k`

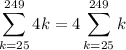
We know how to sum the first
`N` integers, but we need to sum the first 249 integers starting from 25, so we can rewrite our sum using this little trick:

`\displaystyle \sum_(k=25)^(249)k = \sum_(k=1)^(249)k - \sum_(k=1)^(24)k`

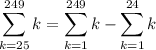
In other words, we're summing all the first 249 integers, but then we remove the first 24. As a result, we have the sum of all integers from 25 to 249:

`1+2+3+\ldots+248+249-(1+2+3+\ldots+23+24) = 25+26+27+\ldots+248+249`

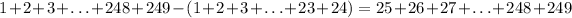
So, we have

`\displaystyle 4\sum_(k=25)^(249)k = 4\left(\sum_(k=1)^(249)k-\sum_(k=1)^(24)k\right)`

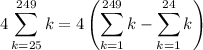
And in both cases we can use the formula

`\displaystyle \sum_(k=1)^(N)k=(N(N+1))/(2)`

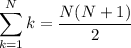
And we have

`\displaystyle 4\left(\sum_(k=1)^(249)k-\sum_(k=1)^(24)k\right)=4\left((249\cdot 250)/(2)-(24\cdot 25)/(2)\right)=2\cdot 249\cdot 250 - 2\cdot 24\cdot 25`

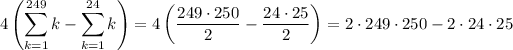
Which evaluates to

`2\cdot 249\cdot 250 - 2\cdot 24\cdot 25 = 124500-1200 = 123.300`