Question

Correct answers only please! If you don't know the answer, then please don't guess or say what you think it is.

Given a student number system for a county requires that the student number be 6 characters.


The first 4 characters are any single digit number but no character can repeat and the last two characters must be a letter and letters cannot be the same. How many unique student numbers are possible?


A. 6,500,000


B. 3,276,000


C. 3,407,040


D. 6,760,000

Answer 1

Answer: B. 3,276,000

Explanation:

Given : A student number system for a county requires that the student number be 6 characters.

Number of digits (0,1,2,3,4,5,6,7,8,9)=10

Number of letters in English alphabet = 26

When repetition of things is not allowed then we use Permutations.

Number of permutations of m things taking n at a time =
`^mP_n=(m!)/((m-n)!)`

Similarly, Number of permutations of 10 numbers taking 4 at a time :

`^(10)P_4=(10!)/((6)!)=(10*9*8*7*6!)/(6!)=5040`

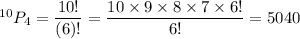
Number of permutations of 26 letters taking 2 at a time :

`^(26)P_2=(26!)/((2)!)=(26*25*24!)/(24!)=650`

Now, the possible number of numbers can be make =
`5040*650=3,276,000`

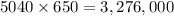
Hence, the correct answer is options (b).