Question

A Boeing 747 "Jumbo Jet" has a length of 59.7 m. The runway on which the plane lands intersects another runway. The width of the intersection is 25.0 m. The plane decelerates through the intersection at a rate of 5.4 m/s2 and clears it with a final speed of 50 m/s. How much time is needed for the plane to clear the intersection?

Answer 1

The plane needs 1,56 seconds to clear the intersection.

Step-by-step explanation:

This is a case of uniformly accelerated rectilinear motion.

`V_0^(2) = V_f^(2) - 2ad`

`V_0=\sqrt{V_0^(2) } = ?`

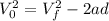
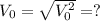
Vf=50 m/s

`V_f^(2)  = (50 m/s)^(2) = 2500  m^(2)/s^(2)`

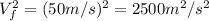
a = -5.4
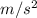`m/s^(2)` (Negative because is decelerating)

d = displacement needed to clear the intersection. It should be the width of the intersection plus the lenght of the plane.

d= 59,7m + 25 m = 84.7 m

Calculating
`V_0`:

`V_0^(2) = V_f^(2) - 2ad`

`V_0^(2)= 2500 (m^(2) )/(s^(2) ) - 2(-5.4(m)/(s^(2) ))(84.7 m)`

`V_0^(2)= 3,414.76 (m^(2) )/(s^(2) )`

`V_0= √(3,414.76) = 58.44 (m)/(s)`

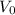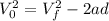
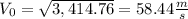
Otherwise:

`t = (V_f-V_0)/(a) =(50(m)/(s) - 58.44(m)/(s)  )/(-5.4 (m)/(s^(2) ) ) = 1.56 s`