Question

Suppose in a society where there are equal numbers of men and women. There is a 50% chance for each child that a couple gives birth to is a girl and the genders of their children are mutually independent. Suppose in this strange and primitive society every couple prefers a girl and they will continue to have more children until they get a girl and once they have a girl they will stop having more children, what will eventually happen to the gender ratio of population in this society?

Answer 1

eventually the gender ratio of population in this society will be 50% male and 50% female.

Explanation:

For practical purposes we will think that every couple is healthy enough to give birth as much children needed until giving birth a girl.

As the problem states, "each couple continue to have more children until they get a girl and once they have a girl they will stop having more children". Then, every couple will have one and only one girl.

1. This girl would be the n-th child with a probability
   `(0.5)^n`.

We will denote for P(Bₙ) the probability of a couple to have exactly n boys.

Observe that statement 1 implies that:

`P(B_(n-1))=(0.5)^(n)`.

Then, the average number of boys per couple is given by

`\sum^(\infty)_(n=1)(n-1)P(B_(n-1))=\sum^(\infty)_(n=1)(n-1)((1)/(2) )^n=\sum^(\infty)_(n=2)n((1)/(2) )^n=\\\\=\sum^(\infty)_(m=2)\sum^(\infty)_(n=m)((1)/(2) )^n=\sum^(\infty)_(m=2)((1)/(2) )^(m-1)=\sum^(\infty)_(m=1)((1)/(2) )^(m)=1.\\`

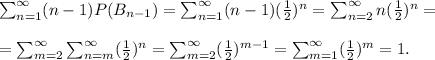
This means that in average every couple has a boy and a girl. Then eventually the gender ratio of population in this society will be 50% male and 50% female.