Answer:
The posterior probability that the lathe tool is properly adjusted is 94.7%
Explanation:
This can be formulated as the following problem:
What is the probability of B happening, knowing that A has happened.
It can be calculated by the following formula
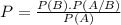
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.
In your problem we have that:
-A is the probability that the part chosen is found to be acceptable.
The problem states that the probability its lathe tool is properly adjusted is 0.8. When it happens, there is a 0.9 probability that the parts produced pass inspection. There is also a 0.2 probability of the lathe is out of adjustment, when it happens the probability of a good part being produced is only 0.2.
So, P(A) = P1 + P2 = 0.8*0.9 + 0.2*0.2 = 0.72 + 0.04 = 0.76
Where P1 is the probability of a good part being produced when lathe tool is properly adjusted and P2 is the probability of a good part being produced when lathe tool is not properly adjusted.
- P(B) is the the probability its lathe tool is properly adjusted. The problem states that P(B) = 0.8
P(A/B) is the probability of A happening given that B has happened. We have that A is the probability that the part chosen is found to be acceptable and B is the probability its lathe tool is properly adjusted. The problem states that when the lathe is properly adjusted, there is a 0.9 probability that the parts produced pass inspection. So P(A/B) = 0.9
So, probability of B happening, knowing that A has happened, where B is the lathe tool is properly adjusted and A is that the part randomly chosen is inspected and found to be acceptable is:

The posterior probability that the lathe tool is properly adjusted is 94.7%