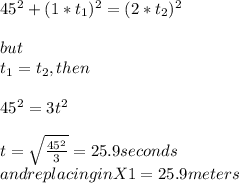Question

A child, who is 45 m from the bank of a river, is being carried helplessly downstream by the river's swift current of 1.0 m/s. As the child passes a lifeguard on the river's bank, the lifeguard starts swimming in a straight line (Fig. 3–46) until she reaches the child at a point downstream. If the lifeguard can swim at a speed of 2.0 m/s relative to the water, how long does it take her to reach the child? How far downstream does the lifeguard intercept the child?

Answer 1

The lifeguard takes 25.9 seconds to reach the child, at 25.9 meters from the start point downstream.

Step-by-step explanation:

As the image shows, the child trajectory, the lifeguard trajectory and the distance from the bank form a triangle. This triangle is formed by the distances, an we already know the distance from the bank and the speed of child, and the speed of the lifeguard. So we have unknom time in common. Lets see the equations:

Using phitagoras theorem

`45^(2)+(1*t_(1) )^(2)  =(2*t_(2) )^(2)\\\\but\\t_(1) =t_(2) , then\\\\45^(2) =3t^(2) \\\\t=\sqrt{(45^(2))/(3)  } = 25.9seconds\\and replacing in X1= 25.9 meters`