Answer:
The equation of the line is
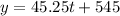
Explanation:
The general for of a line is:
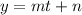 (1)
(1)
where:
 is the slope of the line and
is the slope of the line and
 is the intercept with the axis of the dependent variable,
is the intercept with the axis of the dependent variable,
 in this case.
in this case.
In order to obtain the value of the slope (
 ) we can use the corresponding slope formula:
) we can use the corresponding slope formula:
 (2)
(2)
where
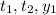 and
and
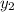 are the corresponding coordinates of the given points. In this case:
are the corresponding coordinates of the given points. In this case:

Substituting these values in equation (2) we obtain:
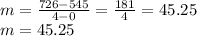
Hence, the line equation is now:
 (3)
(3)
Now to obtain the value of
 you can follow two options:
you can follow two options:
- You can substitute one of your points,
 or
or
 , in equation (3). In this way, you will obtain an equation where the variable is
, in equation (3). In this way, you will obtain an equation where the variable is

Note that for this question, it is easier to select point A because of having the independent variable equals to zero
 . Hence, substituting point A in equation (3):
. Hence, substituting point A in equation (3):

Therefore, the line equation is:
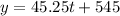
The second option to find
 is to think of the meaning of the intercept. The intercept of a line is defined as the point in which the line crosses the axis of the dependent variable, which also means that the value of the independent variable for this point is zero. From this, we could have automatically said that
is to think of the meaning of the intercept. The intercept of a line is defined as the point in which the line crosses the axis of the dependent variable, which also means that the value of the independent variable for this point is zero. From this, we could have automatically said that
 is equal to
is equal to
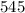 .
.
See the attachment for a plot of the line.