Question

Suppose that a submarine inadvertently sinks to the bottom of the ocean at a depth of 1000m. It is proposed to lower a diving bell to the submarine and attempt to enter the conning tower. What must the minimum air pressure be in the diving bell at the level of the submarine to prevent water from entering into the bell when the opening valve at the bottom is cracked open slightly? Give your answer in absolute kilopascal. Assume that seawater has a constant density of 1.024 g/cm3.

Answer 1

1.004 × 10⁴ kPa

Step-by-step explanation:

Given data

• Depth (h): 1000 m

• Density of seawater (ρ): 1.024 × 10³ kg/m³

`(1.024g)/(cm^(3)).(1kg)/(10^(3)g) .(10^(6)cm^(3))/(1m^(3) ) =1.024 * 10^(3) kg/m^(3)`

• Gravity (g): 9.806 m/s²

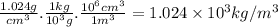
In order to prevent water from entering, the air pressure must be equal to the pressure exerted by the seawater at the bottom. We can find that pressure (P) using the following expression.

P = ρ × g × h

P = (1.024 × 10³ kg/m³) × (9.806 m/s²) × 1000 m

P = 1.004 × 10⁷ Pa

P = 1.004 × 10⁷ Pa × (1 kPa/ 10³ Pa)

P = 1.004 × 10⁴ kPa

Answer 2

P=10.04Mpa

Step-by-step explanation:

the minimum air pressure must be equal to the water pressure at that depth, to calculate the pressure we can use the following equation

P=hgρ

where

h=depth=1000m

g=gravity=9.81m/s^2

ρ=density=1.024g/cm^3=1024kg/m^3

P=pressure

P=(1000)(9.81)(1024)=10045440Pa=10.04Mpa