Question

Because Earth's rotation is gradually slowing, the length of each day increases: The day at the end of 1.0 century is 1.0 ms longer than the day at the start of the century. In 43 centuries, what is the total of the daily increases in time (that is, the sum of the gain on the first day, the gain on the second day, etc.)?

Answer 1

0.043 seconds

2.7378×10⁻⁸ seconds

Step-by-step explanation:

In the question it is given each century adds 1 ms to a day due to the slowing rotation of the Earth

In 43 centuries the length of the first day of the year will be

43 × 1 = 43 ms = 0.043 seconds

1 ms = 1 century

1 century = 100 years × 365.25 days

⇒1 ms = 36525 days

`1\ day=(1)/(36525)=2.7378* 10^(-5) ms=2.7378* 10^(-8) s`

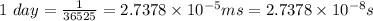
Sum of the gain on the first day would be

0.043 + 2.7378×10⁻⁸ = 0.04300000273785 second

Sum of the gain on the second day would be

0.043 + 2.7378×10⁻⁸+2.7378×10⁻⁸ = 0.04300054757 seconds

The increase in each day would be 2.7378×10⁻⁸ seconds