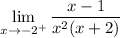
The limit is infinite because the denominator approaches 0 while the numerator does not, since
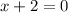 when
when
 . Which infinity it approaches (positive or negative) depends on the sign of the other terms for values of
. Which infinity it approaches (positive or negative) depends on the sign of the other terms for values of
 near -2.
near -2.
Since
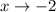 from the right, we're considering values of
from the right, we're considering values of
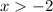 . For example, if
. For example, if
 , then
, then
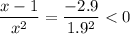 ; if
; if
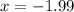 , then
, then
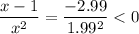 , and so on. We can keep picking values of
, and so on. We can keep picking values of
 that get closer and closer to -2, and we would see that
that get closer and closer to -2, and we would see that
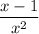 contributes a negative sign every time. So the limit must be
contributes a negative sign every time. So the limit must be
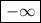 .
.
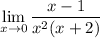
By similar reasoning above, we see that
 contributes a negative sign regardless of which side we approach 0 from.
contributes a negative sign regardless of which side we approach 0 from.
 is always negative and
is always negative and
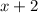 is always positive, so the net effect is a negative sign and the limit from either side is
is always positive, so the net effect is a negative sign and the limit from either side is
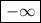 .
.
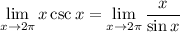
Direct substitution gives 0 in the denominator. For
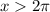 we have
we have
 , and for
, and for
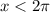 we have
we have
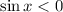 . Meanwhile, the numerator stays positive, which means the limit is positive or negative infinity depending on the direction in which
. Meanwhile, the numerator stays positive, which means the limit is positive or negative infinity depending on the direction in which
 approaches
approaches
 , so this limit does not exist.
, so this limit does not exist.