Question

You buy a ten-year bond with an 8% coupon rate at a yield-to-maturity of 6%. (Both rates follow the BEY convention.) You hold the bond for two years, reinvesting coupons in a money market account earning an APR of 4%, compounded monthly. On the day you receive the fourth coupon, you sell the bond. Since market interest rates have increased, you sell it at a yield-to-maturity of 8%. What is your realized compound yield? Report the realized compound yield as an APR with semi-annual compounding.

Answer 1

Ans. the realized yield is 0.7749% APR semi-annual compounding

Step-by-step explanation:

Hello, first we need to find the exact amount paid for this bond, you can find this by finding the coupon that it pays every 6 months and transforming the effective annual rate of the YTM into semi-annual effective rate. All this as follows.

`Coupon=FaceValue*(AnnualCouponRate)/(2)=1000*(0.08)/(2)=40`

`YTM(SemiAnnual)=(1+YTM(annual))^{(1)/(2) } -1=(1+0.06)^{(1)/(2) } -1=0.0296`

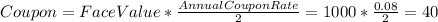
Ok, so far, our semi annual coupon is $40 and our semi-annual YTM is 2.96%. Now. we are ready to find the price paid for the bond.

`Price=(Coupon((1+YTM)^(n-1)-1) )/(YTM(1+YTM)^(n-1) ) +((FaceValue+Coupon))/((1+YTM)^(n) )`}

`Price=(40((1+0.0296)^(19)-1) )/(40(1+0.0296)^(19) ) +((1000+40))/((1+0.0296)^(20) ) =1155.91`

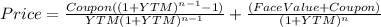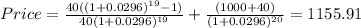
4 bonds were received and placed in a money market account earning a 4% compounded monthly rate, in order to make things more simple, let´s convert this into a semi-annual effective rate, since the bonds are paid every 6 months. Like this.

`r(semi-annual)=(1+(0.04)/(12) )^(6) -1=0.020167`

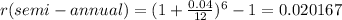
Since you received 4 coupons, we have to find the future value of this 4 coupons, that is:

`FV(Coupons)=40(1+0.020167)^(3)+ 40(1+0.020167)^(2)+40(1+0.020167)^(1)+40`}

`FV(Coupons)=164.91`

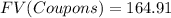
The selling price of the bond, given the new YTM=8% is:

`Price=(40((1+0.03923)^(15)-1) )/(40(1+0.03923)^(15) ) +((1000+40))/((1+0.03923)^(16) ) =1009.02`

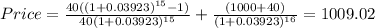
Adding both values (sell price of the bond and future values of the coupons) we get the money inflow, what we will call from here FV. The persent value is the money you first paid for the bond.

And then we find the rate of return of all this transactions by using this formula.

`\sqrt[2]{(FV)/(PV) }-1=r`
`\sqrt[2]{((1009.02+164.91)/(1155.91) }-1=r =0.0077638`

The return of this invesment is 0.77638% effective annually, but we need it to have a semi-annual compounding, so first, we need to turn this effective annual rate into an effective semi annual rate and them, multiply by 2. this is the math of all this.

`EffectiveSemi-annnual=(1+0.0077638)^{(1)/(2) } -1=0.0038744`

`APR(SemiAnnualComp)=0.0038744*2=0.007749`

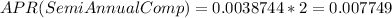
APR(SemiAnnualComp)= 0.7749%

Best of luck.