Answer:
4.933m/s
Step-by-step explanation:
the wagon has a weight of 35.1kg*9.81m/s2 = 343.98N
of that weight 343.98N*sin(18.3)=108N are parallel to the hill and oposit tothe tension of the rope.
then, the force that is moving the wagon is 125N-108N=17N
F=m*a then 17N=35.1kg*a
a=0.4843 m/s2
we have two equations

then
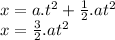

t=10.188s
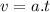
v=4.933 m/s