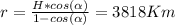Question

Suppose that, while lying on a beach near the equator of a far-off planet watching the sun set over a calm ocean, you start a stopwatch just as the top of the sun disappears. You then stand, elevating your eyes by a height H = 1.43 m, and stop the watch when the top of the sun again disappears. If the elapsed time is it = 11.9 s, what is the radius r of the planet to two significant figures? Notice that duration of a solar day at the far-off planet is the same that is on Earth.

Answer 1

R=3818Km

Step-by-step explanation:

Take a look at the picture. Point A is when you start the stopwatch. Then you stand, the planet rotates an angle α and you are standing at point B.

Since you travel 2π radians in 24H, the angle can be calculated as:

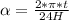`\alpha =(2*\pi *t)/(24H)` t being expressed in hours.

`\alpha =(2*\pi *11.9s*1H/3600s)/(24H)=0.000865rad`

From the triangle formed by A,B and the center of the planet, we know that:

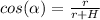`cos(\alpha )=(r)/(r+H)` Solving for r, we get:

`r=(H*cos(\alpha) )/(1-cos(\alpha) ) =3818Km`