Question

On rainy days, Izzy goes from his house to the school by running 1.2 miles on West St, then makes a 90º turn and runs 0.5 miles on North Ave.

a. If Izzy runs 7.5 miles per hour, approximately how much time will it take her to run to school on rainy days?

b. On dry days, Izzy runs on the dashed path through the woods. How far is she traveling?

c. If Izzy runs 7.5 miles per hour, how much time will she save by cutting through the woods?

Answer 1

a) It will take Izzy 0.226 hours = 13.6 minutes = 13 minutes 36 seconds to run to school on dashed days.

b) Izzy runs 1.30 miles on dry days.

c) Izzy saves 3 minutes and 12 seconds cutting through the woods.

Explanation:

This problem can be solved by a simpe rule of three problem.

a) On rainy days, she runs 1.2 + 0.5 = 1.7 miles.

The problem states that for rainy days, she runs 7.5 miles per hour. We know that in a hour, Izzy will run 7.5 miles. We want to know how long it takes for her to run 1.7 miles. So

1 hour - 7.5 miles

x hours - 1.7 miles

7.5x = 1.7

`x = (1.7)/(7.5)`

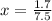
x = 0.226 hours

It will take Izzy 0.226 hours = 13.6 minutes = 13 minutes 36 seconds to run to school on dashed days.

b) Now we have a right triangle, where the sides are the 1.2 miles and the 0.5miles, and the path through the woods x is the hypotenuse.

So, we apply the pythagorean theorem.

`x^(2) = (1.2)^(2) + (0.5)^(2)`

`x^(2) = 1.44 + 0.25`

`x^(2) = 1.69`

`x = 1.30`

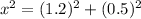
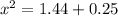
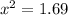
So, Izzy runs 1.30 miles on dry days.

c) The first step for this question is knowing how long it takes for Izzy to run 1.30 miles at 7.50 miles a hour. So:

1 hour - 7.50 miles

x hours = 1.30 miles

7.50x = 1.30

`x = (1.3)/(7.5)`

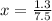
x = 0.173 hours

So, it takes Izzy 0.173 hours = 10.4 minutes = 10 minutes 24 seconds to run through the woods.

13' 36''

-10' 24''

3' 12''

Izzy saves 3 minutes and 12 seconds cutting through the woods.