Question

Consider the three functions below.

f(x) = Negative StartFraction 6 Over 11 EndFraction (eleven-halves) Superscript x g(x) = StartFraction 6 Over 11 EndFraction (eleven-halves) Superscript negative x h(x) = Negative StartFraction 6 Over 11 EndFraction (eleven-halves) Superscript negative x

Which statement is true?

The range of h(x) is y > 0.
The domain of g(x) is y > 0.
The ranges of f(x) and h(x) are different from the range of g(x).
The domains of f(x) and g(x) are different from the domain of h(x).

Answer 1

The range of g(x) is y > 0

The ranges of f(x) and h(x) are different from the range of g(x)

Explanation:

we have

`f(x)=-((6)/(11))^(x)`

`g(x)=((6)/(11))^(-x)`

`h(x)=-((6)/(11))^(-x)`

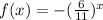
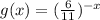
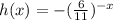
Using a graphing tool

see the attached figure

Verify each statement

case A) The range of h(x) is y > 0.

The statement is false

The range of h(x) < 0

case B) The range of g(x) is y > 0. (Note the statement is The range of g(x) is y > 0 instead of The domain of g(x) is y > 0)

The statement is true (see the attached figure)

case C) The ranges of f(x) and h(x) are different from the range of g(x)

The statement is true (see the attached figure)

Because

The ranges of f(x) and h(x) are y < 0

and

The range of g(x) is y > 0

case D) The domains of f(x) and g(x) are different from the domain of h(x)

The statement is false

The domain of the three functions is the same

Answer 2

OPTION C.The ranges of f(x) and h(x) are different from the range of g(x).

Explanation: