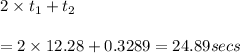Question

The height of a helicopter above the ground is given by h = 3.30t3, where h is in meters and t is in seconds. At t = 2.30 s, the helicopter releases a small mailbag. How long after its release does the mailbag reach the ground? 9.857 Incorrect: Your answer is incorrect.

Answer 1

The total time to reach ground is 24.89 seconds

Step-by-step explanation:

Since the height of the helicopter is given by

`h(t)=3.30t^(3)` thus at time t = 2.30 seconds the height of the helicopter is

`h(2.30)=3.30* (2.30)^(3)=40.151m`

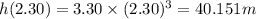
The velocity of helicopter upwards at time t = 2.30 is given by

`v=(dh(t))/(dt)\\\\v=(d)/(dt)(3.30t^(3))\\\\v(t)=9.90t^(2)\\\\\therefore v(2.30)=9.90* (2.30)^2=120.45m/s`

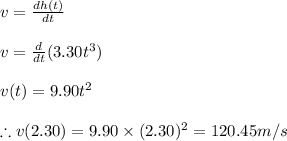
Now the time after which it becomes zero can be obtained using the equations of kinematics as

1) Time taken by the mailbag to reach highest point equals

`v=u+gt\\\\0=120.45-9.81* t\\\\\therefore t_(1)=(120.45)/(9.81)=12.28s`

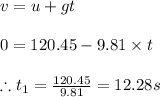
2) Time taken by the mailbag to reach ground from a height of 40.151 meters equals

`s=ut+(1)/(2)gt^(2)\\\\40.151=120.45t+4.9t^(2)`

Solving for t we get
`t_(2)=0.3289secs`

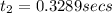
Now the total time of the journey is

`\\\\2* t_(1)+t_(2)\\\\=2* 12.28+0.3289=24.89secs`