Question

Happy Trails, a bicycle rental company, is considering purchasing three additional bicycles. Each bicycle would cost them $249.66. At the end of the first year the increase to their revenues would be $140 per bicycle. At the end of the second year the increase to their revenues would be $115 per bicycle and they can sell each used bike for another $25. At which of the following interest rates is the sum of the present value of the revenues from buying a bicycle closest to the price of a bicycle?

a. 5 percent
b. 6 percent
c. 7 percent
d. 8 percent

Answer 1

The sum of the present value of the revenues from buying a bicycle is the closest to the price of a bicycle when we use an interest rate of:

d. 8 percent.

Step-by-step explanation:

Making use of the present value concept is a useful way to compare cases where money is to be received in the future. The higher the present value, the better.

• In this case, we don't know the sum of the present value of the revenues from buying one bicycle, so we have to determine it by using different interest rates (a. 5%, b. 6%, c. 7%, and d. 8%).

• Each time we determine a present value, we will compare it with the price of a bicycle ($249.66), to see at which interest rate is the present value closest to the price of the bicycle.
• Since we can sell the used bike for $25 at the end of the second year, we can add this money to the revenues of the second year ($115), to simplify calculations. We should then get a total of $115+$25=$140 by the end of the second year.
• The following formula is the one that we are going to use to determine our present value for each interest rate:

`P=(C)/((1+r)^(n) )\\`

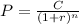
Where P: Present value (what we are going to determine),

C: Cash flow at a given period of time (what we are going to receive by the end of a given year; in this case, $140 for the first year, C₁, and another $140 for the second year, C₂),

r: Interest rate (we will use the different mentioned options of 5%, 6%, 7%, and 8%, or 0.05, 0.06, 0.07, and 0.08, respectively, until we get a present value that is the closest possible to the price of a bicycle), and

n: Number of periods of time (in this case, n=1 for the first year, and n=2 for the second year).

Now, since we are getting money twice (each year for two years), we can add the term for the second year to the formula, and we will get something like this:

`P=(C_(1))/((1+r)^(1) )+(C_(2))/((1+r)^(2) )\\\\P=(C_(1))/(1+r )+(C_(2))/((1+r)^(2) )\\\\P=(140dollars)/(1+r )+(140dollars)/((1+r)^(2) )\\\\P=140dollars*[(1)/(1+r )+(1)/((1+r)^(2) )]`

We could further simplify our formula but it's better not complicate ourselves so much.

-------------------------------------------------------------------------------------------------------

Let's now start determining our present value of the revenues with the interest rate of 5%, or 0.05:

`P_(r:0.05)=140dollars*[(1)/(1+0.05)+(1)/((1+0.05)^(2) )]\\\\P_(r:0.05)=140dollars*[(1)/(1.05)+(1)/(1.1025)]\\\\P_(r:0.05)=140dollars*[0.95238+0.90703]\\\\P_(r:0.05)=140dollars*1.85941\\\\P_(r:0.05)=260.31733dollars`

So we got a present value of P=$260.32 while using an interest rate of 5%, which is pretty close to the price of $249.66, but maybe not close enough. We should determine the difference between the present value and the price like this:

`Difference=260.32dollars-249.66dollars\\Difference=10.66dollars`

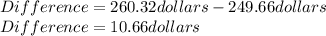
The less difference there is, the closer we get to the price of the bicycle. Let's use the following interest rate now.

-------------------------------------------------------------------------------------------------------

6%, or 0.06:

`P_(r:0.06)=140dollars*[(1)/(1+0.06)+(1)/((1+0.06)^(2) )]\\\\P_(r:0.06)=140dollars*[(1)/(1.06)+(1)/(1.1236)]\\\\P_(r:0.06)=140dollars*[0.94340+0.89000]\\\\P_(r:0.06)=140dollars*1.83340\\\\P_(r:0.06)=256.67550dollars`

In the 6% interest rate case, our present value is of P=$256.68, which got us closer to the price of $249.66. We should calculate its difference with the price:

`Difference=256.68dollars-249.66dollars\\Difference=7.02dollars`

-------------------------------------------------------------------------------------------------------

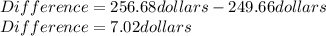
7%, or 0.07:

`P_(r:0.07)=140dollars*[(1)/(1+0.07)+(1)/((1+0.07)^(2) )]\\\\P_(r:0.07)=140dollars*[(1)/(1.07)+(1)/(1.1449)]\\\\P_(r:0.07)=140dollars*[0.93458+0.87344]\\\\P_(r:0.07)=140dollars*1.80802\\\\P_(r:0.07)=253.12262dollars`

The 7% case gave us a present value of P=$253.12. Its difference with the price is:

`Difference=253.12dollars-249.66dollars\\Difference=3.46dollars`

-------------------------------------------------------------------------------------------------------

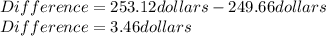
8%, or 0.08:

`P_(r:0.08)=140dollars*[(1)/(1+0.08)+(1)/((1+0.08)^(2) )]\\\\P_(r:0.08)=140dollars*[(1)/(1.08)+(1)/(1.1664)]\\\\P_(r:0.08)=140dollars*[0.92593+0.85734]\\\\P_(r:0.08)=140dollars*1.78327\\\\P_(r:0.08)=249.65763dollars`

This time, by using an interest rate of 8%, we got to the present value of P=$249.66, which is exactly the price of a bicycle. The difference in this case is therefore 0.

-------------------------------------------------------------------------------------------------------

So the sum of the present value of the revenues from buying a bicycle is the closest to the price of a bicycle when we use an interest rate of:

d. 8 percent.