Question

The reaction described by the equation CH 3 Cl + NaOH → CH 3 OH + NaCl follows the second-order rate law, rate = k [ CH 3 Cl ] [ NaOH ] . When this reaction is carried out with starting concentrations [ CH 3 Cl ] = 0.2 M and [ NaOH ] = 1.0 M , the measured rate is 1 × 10 − 4 mol L − 1 s − 1 . What is the rate after one-half of the CH 3 Cl has been consumed? (Caution: The initial concentrations of the starting materials are not identical in this experiment. Hint: Determine how much of the NaOH has been consumed at this point and what its new concentration is, compared with its initial concentration.)

Answer 1

The rate is
`4,5 * 10^(-5)(mole)/(Ls)`

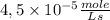
Step-by-step explanation:

Stoichiometry

`CH_(3)Cl+NaOH \rightarrow CH_(3)OH+NaCl`

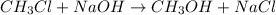
Kinetics

`-r_(A)=k * [CH_(3)Cl] * [NaOH]`

The rate constant K can be calculated by replacing with the initial data

`1 * 10^(-4)(mole)/(Ls)=k * [0,2M] * [1,0M]  =5 * 10^(-4)(L)/(mole s)`

Taking as a base of calculus 1L, when half of the
`CH_(3)Cl` is consumed the mixture is composed by

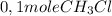`0,1 mole CH_(3)Cl` (half is consumed)

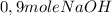`0,9 mole NaOH` (by stoicheometry)

`0,1 mole CH_(3)OH`

`0,1 mole NaCl`

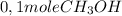
Then, the rate is

`-r_(A)=5 * 10^(-4) (L)/(mole s)* 0,1M * 0,9 M=4,5 * 10^(-5)(mole)/(Ls)`

The reaction rate decreases because there’s a smaller concentration of reactives.