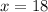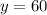Question

A right triangle whose base is 30 units is divided into two parts by a line drawn parallel to the base. It is given that the resulting right trapezoid has an area larger by 7,0 (which is sexagesimal) = 420 than the upper triangle, and that the difference between the height y of the upper triangle and the height z of the trapezoid is 20. if x is the length fo the upper base of the trapezoid, these statement lead to the relations 1/2z (x+30) = 1/2xy + 420, y - z = 20. The problem calls for finding the values of the unknown quantities x, y, and z. [Hint: By properties of similar triangles, y/(y+z) = x/30.]

Answer 1

`x=18`

`y=60`

`z=40`

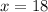
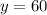
Explanation:

From the relations stablished in the problem we have the following equation system:

`y-z=20` (equation 1)

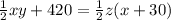`(1)/(2) xy+420=(1)/(2)z(x+30)` (equation 2)

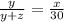`(y)/(y+z) =(x)/(30)` (equation 3)

From equation 1 we can find an expression of
`y` in terms of
`z` which we're going to call equation 4

`y-z=20`

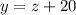`y=z+20` (equation 4)

We can then replace the equation 4 in the equation 2 in order to find an expression of
`x` in terms of
`z`

`(1)/(2) xy+420=(1)/(2)z(x+30)`

`(1)/(2) (xy+840)=(1)/(2)z(x+30)`

`xy+840=z(x+30)`

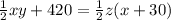
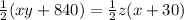
`x(z+20)+840=z(x+30)` (here we replaced the eq.4)

`xz+20x+840=xz+30x`

`xz+20x-xz=30z-840`

`20x=30z-840`

`10(2x)=10(3z-84)`

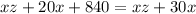
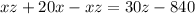
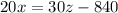
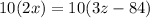
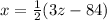`x=(1)/(2) (3z-84)` (equation 5)

Now, we can replace equations 4 & 5 inside the equation 3 so we can find the value of
`z`

`(y)/(y+z) =(x)/(30)`

`(z+20)/(z+20+z) =(1)/(30)*(1)/(2) (3z-84)`

`(z+20)/(2z+20) =(1)/(30)*(1)/(2) (3z-84)`

`(z+20)/(2(z+10)) =(1)/(2)*(1)/(30) (3z-84)`

`(1)/(2)*(z+20)/(z+10) =(1)/(2)*(1)/(30) (3z-84)`

`(z+20)/(z+10) =(1)/(10) ((3z)/(3)-(84)/(3))`

`(z+20)/(z+10) =(1)/(10) (z-28)`

`z+20 =(1)/(10) (z-28)*(z+10)`

`10(z+20) =z^(2)+10z-28z-280`

`10z+200 =z^(2)-18z-280`

`z^(2)-28z-480=0`

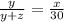
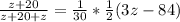
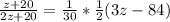
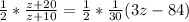
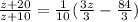
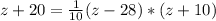
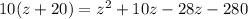
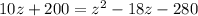
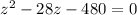
This is a quadratic equation which has the form
`a*z^(2) +b*z+c=0`

where

`a=1`

`b=-28`

`c=-480`

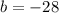
Then, we can find the solutions to this quadratic equation using the well-know quadatric formula which says that

`z=(-b)/(2a)`±
`\frac{\sqrt{b^(2)-4ac} }{2a}`

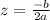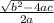
then, replacing the values of a, b and c we find the values of z

`z_(1)=\frac{-(-28)+\sqrt{(-28)^(2)-4(1)(-480)} }{2(1)}`

`z_(1)=40`

`z_(2)=\frac{-(-28)-\sqrt{(-28)^(2)-4(1)(-480)} }{2(1)}`

`z_(2)=-12`

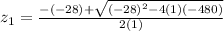
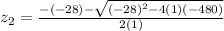
We have two possible values of z, but because we're trying to find the measure of trapezoid's height the result shouldn't be negative, so we keep only the positive value of z, then

`z=40`

Now we may replace this value of z in the equations 4 & 5 in order to find the values of x & y.

`y=z+20` (equation 4)

`y=40+20`

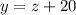`y=60`

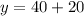
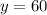
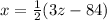`x=(1)/(2) (3z-84)` (equation 5)

`x=(1)/(2) (3(40)-84)`

`x=18`

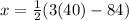
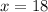
So we've found the values of x, y, and z.

`x=18`

`y=60`

`z=40`