Question

You are an industrial engineer with a shipping company. As part of the package- handling system, a small box with mass 1.60 kg is placed against a light spring that is compressed 0.280 m. The spring has force constant 48.0 N/m . The spring and box are released from rest, and the box travels along a horizontal surface for which the coefficient of kinetic friction with the box is μk = 0.300. When the box has traveled 0.280 m and the spring has reached its equilibrium length, the box loses contact with the spring. (a) What is the speed of the box at the instant when it leaves the spring? (b) What is the maximum speed of the box during its motion?

Answer 1

a) V = 0.82m/s

b) Vmax = 0.985 m/s

Step-by-step explanation:

By conservation of energy we know that:

Eo = Ef
`(m*V^(2))/(2)-(K*Xmax^(2))/(2)=-Ff*Xmax`

Solving for V we get:

V = 0.82 m/s

To find the maximum speed we will do the same to an intermediate point where the compression is X and the distance for the work donde by frictions is given by (Xmax - X) = (0.28m - X):

`(m*Vmax^(2))/(2)+(K*X^(2))/(2)-(K*Xmax^(2))/(2)=-Ff*(Xmax-X)`

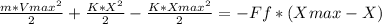
Then we have to solve for V, derive and equal zero in order to find position X. After solving the derivative we get:

X = 0.1m Replacing this value into the equation for Vmax:

Vmax = 0.985m/s