Question

An object moving due to gravity can be described by the motion equation y=y0+v0t−12gt2, where t is time, y is the height at that time, y0 is the initial height (at t=0), v0 is the initial velocity, and g=9.8m/s2 (the acceleration due to gravity). If you stand at the edge of a cliff that is 75 m high and throw a rock directly up into the air with a velocity of 20 m/s, at what time will the rock hit the ground? (Note: The Quadratic Formula will give two answers, but only one of them is reasonable.) View Available Hint(s)

Answer 1

Answer: 6.45 s

Step-by-step explanation:

We have the following equation:

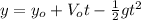`y=y_(o)+V_(o)t-(1)/(2)gt^(2)` (1)

Where:

`y=0` is the height when the rock hits the ground

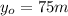`y_(o)=75 m` the height at the edge of the cilff

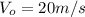`V_(o)=20 m/s` the initial velocity

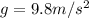`g=9.8 m/s^(2)` acceleration due gravity

`t` time

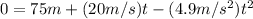`0=75 m+(20 m/s)t-(4.9 m/s^(2))t^(2)` (2)

Rearranging the equation:

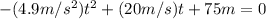`-(4.9 m/s^(2))t^(2) + (20 m/s)t + 75 m=0` (3)

At this point we have a quadratic equation of the form
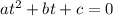`at^(2)+bt+c=0`, and we have to use the quadratic formula if we want to find
`t`:

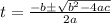`t=\frac{-b\pm\sqrt{b^(2)-4ac}}{2a}` (4)

Where
`a=-4.9`,
`b=20`,
`c=75`

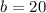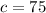
Substituting the known values and choosing the positive result of the equation:

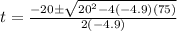`t=\frac{-20\pm\sqrt{20^(2)-4(-4.9)(75)}}{2(-4.9)}` (5)

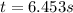`t=6.453 s` This is the time it takes to the rock to hit the ground